A túlélési elemzés pythonban egy üzleti példa nyomán
Előző blogposztunkban megismerkedtünk a túlélési elemzés (survival analysis) alkalmazásaival. A túlélési elemzés statisztikai módszerei a nevükkel ellentétben nem csak orvosi, biológiai kutatásokban hasznosak, hanem minden olyan adathalmaz esetén relevánsak, ahol valamilyen esemény bekövetkezéséhez szükséges időt kell megbecsülni. A következőkben az alkalmazások és az alapötlet után egy üzleti példán mutatjuk be a túlélési elemzés lehetséges megvalósítását pythonban, és áttekintjük néhány túlélési elemzési modell alapötletét is.

Tartsuk meg az ügyfeleinket!
A fenti jelmondattal az üzleti példánk legyen a telekommunikációs, vagy média cégek esete, akik a vásárlók vagy ügyfelek megtartását célzó kampányokat folytatnak. A túlélési elemzés segítségével megbecsülhetjük például azt az időtartamot, amikor az ügyfél várhatóan leiratkozik a szolgáltatásról, elhagyja azt (churn analízis). A továbbiakban bemutatott elemzésekhez a kaggle.com Telco Customer Churn adathalmazát használjuk. Az adathalmazban az egyes sorok az egyes ügyfelekhez tartoznak, akikről ismert néhány tulajdonság (szerződés típusa, milyen szolgáltatásokat vesz igénybe, stb.). A célesemény vagy halál esemény ez esetben a churn, azaz amikor egy ügyfél elhagyja a szolgáltatást, másikra vált. A születési esemény a szerződéskötés kezdete, így az egyes ügyfelek esetén azt az időt mérjük, ameddig használta a szolgáltatást. A célunk, hogy a felhasználók egyes csoportjaira megbecsüljük azt az időt, ameddig a churn nem következik be.
A példánkat egy hagyományos regressziótól az különbözteti meg, hogy vannak úgynevezett cenzorált ügyfelek, akik esetén a céleseményt nem figyeltük meg. Lehetnek olyan kuncsaftok, akik időközben elhunytak, így nem tudjuk, meddig használták volna még a szolgáltatást, illetve olyanok is, akik esetén a churn eddig nem történt meg, de nem tudhatjuk, hogy a jövőben be fog-e következni. A túlélési elemzés eszközei lehetővé teszik, hogy ezen cenzorált felhasználókat is figyelembe vegyük az adatelemzés során. A célunk az, hogy megvizsgáljuk az egyes ügyfélcsoportok túlélési tulajdonságait, hogy az ezekből nyert információkkal és az adatelemzés során levont következtetésekkel a vizsgált cég időben be tudjon avatkozni és ösztönző, célzottabb kampányokkal nagyobb sikerrel tudja megtartani az ügyfeleit.
A túlélési függvény nyomában
A túlélési elemzések során a legtöbb modell az ún. túlélési függvényt (survival function) szeretné megbecsülni. Ez a függvény egy adott időpillanatban megadja annak a valószínűségét, hogy a célesemény még nem történt meg. A kezdeti időpillanatban, amikor a példánkban az ügyfelek elkezdik használni a szolgáltatást, akkor a túlélési függvény értéke 1, hiszen ekkor még egyetlen ügyfél esetén sem figyeltük meg a churn eseményt. Ahogy telik az idő, a túlélési függvény nullára csökken, hiszen egy idő után minden ügyfél vagy szolgáltatót vált, vagy meghal.
Ha van valamilyen feltevésünk a célesemény bekövetkezéséig eltelt idő eloszlására vonatkozóan, akkor a túlélési modellezés eszköztára számos paraméteres modellt kínál fel számunkra, amelyekkel a túlélési függvény megbecsülhető. Pythonban megannyi függvénykönyvtár segíti a túlélési modellezést, érdemes körülnézni a lifelines, a scikit-survival és a pysurvival csomagok által felkínált függvények és modellek között. Ha nem ismerjük, hogy milyen eloszlásból jöhetnek a céleseményig eltelt idők, érdemes nemparaméteres modelleket választanunk. Közülük az ún. Kaplan-Meier modell a legegyszerűbb választás, amely a túlélési valószínűségek időbeli leírását teszi lehetővé.
A Kaplan-Meier modell az egész populáció túlélési függvényét becsüli meg 2 információ – a céleseményig eltelt idő, és a célesemény bekövetkezését leíró bináris változó – alapján. Előnye, hogy minden megfigyelést, azaz esetünkben a cenzorált ügyfeleket is figyelembe veszi a túlélési függvény számításánál. A modell hátránya természetesen az egyszerűségében keresendő, például hogy minden ügyfélre egyenlő túlélési valószínűséget feltételez. A Kaplan-Meier becslőre a legkönnyebben használható implementációt pythonban a lifelines csomagban találjuk, a későbbiekben is ezzel fogunk dolgozni.Miután betöltjük a kaggle.com Telco Customer Churn adathalmazát, a lefelines csomag KaplanMeierFitter modelljével az adathalmaz ‘tenure’ (azaz a céleseményig eltelt időtartam) és ‘Churn’ (a churn bekövetkezését leró bináris változója) alapján számoljuk ki az adathalmazban található összes ügyfél túlélési függvényét, melyet a plot() függvénnyel gyorsan vizualizálhatunk is.
import pandas as pd
from lifelines import KaplanMeierFitter
churn = pd.read_csv("Kaggle-Telco-Customer-Churn.csv")
km = KaplanMeierFitter()
km.fit(churn['tenure'], churn['Churn'], label='Kaplan-Meier estimate')
km.plot()
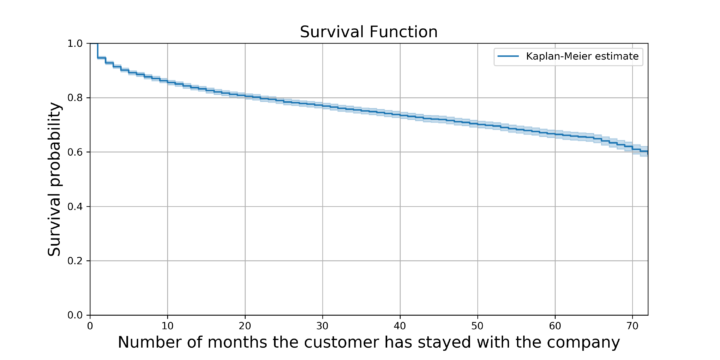
Forrás: Dmlab
A túlélési függvényen jól láthatók annak jellegzetességei: 1-ről indul és folyamatosan csökken. 1 év után az összes ügyfelet vizsgálva annak a valószínűsége, hogy nem történt meg a churn 0.84. Megfigyelhetjük, hogy a túlélési függvényben van egy hirtelen ugrás az 1. hónap után, erre a későbbiekben még visszatérünk.
Cox-regresszió
A Kaplan-Meier modellel egyszerre csak egy csoport vizsgálható, pedig előfordulhat, hogy kíváncsiak vagyunk az egyes egyének túlélési függvényeire. További limitáció, hogy a Kaplan-Meier modellben nem tudunk figyelembe venni további magyarázó változókat. Ezen hiányosságokat aknázza ki a túlélési elemzés egyik legnépszerűbb eszköze, a Cox-regresszió. A Cox-regresszióval több magyarázó változót is be lehet vonni a modellezésbe és azok fontosságát a regresszióhoz hasonló együtthatókkal összehasonlítani.
A Cox-regresszió az ún. hazárd függvény (hazard function) vagy veszélyességi függvény, pontosabban ezen függvény értékeinek logaritmusát modellezve számolja ki a túlélési függvényeket. A hazárd függvény egy adott időpillanatban megadja annak a valószínűségét, hogy most következik be a célesemény feltéve, hogy eddig még nem következett be. A pontos matematikai megfogalmazás és képletek helyett (lásd referenciák) nézzük meg, milyen egyszerű pythonban a lifelines függvénykönyvtár segítségével Cox-regressziót illeszteni a vizsgált churn adathalmazunkra. Az alábbi kódrészletben pythonban a lifelines függvénykönyvtár a CoxPHFitter.fit() függvényének segítségével hajtjuk végre a Cox-regressziót, majd a regresszió paramétereit a print_summary() és plot() függvényekkel írhatjuk ki és vizualizálhatjuk.
from lifelines import CoxPHFitter
cph = CoxPHFitter()
cph.fit(churn, duration_col='tenure', event_col='Churn')
cph.print_summary()
cph.plot()
A Cox-modellből levont következtetésekhez nem közvetlenül a hazárd függvényt, hanem a hazárd arányokat becsüljük, amikkel az egyes csoportokat összehasonlíthatjuk és megvizsgálhatjuk az egyes magyarázó változók hatását. Az egyes változókhoz tartozó hazárd arányokat a következőképpen kaphatjuk meg.
cph.hazard_ratios_
A hazárd arányokból (hazard ratio) arról kaphatunk információt, hogy egy referencia csoporthoz képest mekkora a célesemény bekövetkezésének kockázata. Ha ez kisebb, mint 1, akkor nagyobb a kockázat, így az adott magyarázó változó rövidebb medián túlélési időket okoz.
A Cox modellel akár az egyes ügyfelekre egyenként is kirajzolhatjuk a túlélési függvényt, valamint azt is vizsgálhatjuk, hogy hogyan változik a túlélési függvény az egyes magyarázó változók különböző értékeinél. Nézzük meg, hogy a szerződés típusa (Contract) változó értékei szerint hogyan módosul a túlélési függvény!
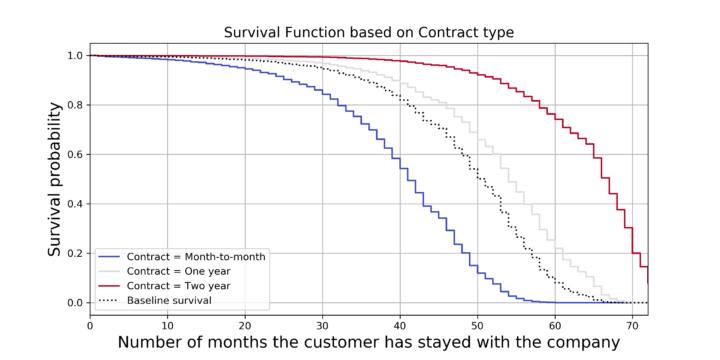
Forrás: Dmlab
Az ábrán jól látható, hogy három féle szerződés típust különböztethetünk meg, havi (kék), éves (szürke) vagy kétéves (piros) szerződéssel rendelkező ügyfeleket. A havi szerződéssel rendelkezők túlélési függvénye hamarabb levág, ezen ügyfelek esetén következik be várhatóan leghamarabb a churn. Ha visszaemlékszünk, a Kaplan-Meier becslőben is az első hónap után tapasztaltunk egy nagyobb ugrást, ami szintén a havi szerződéssel rendelkező ügyfelek churn-jét mutatta.
A Cox-regresszióval a túlélési elemzésben figyelembe vehetők a magyarázó változók, és ahogy a szerződés típusra látott példán szemléltettük, vizsgálható azok különböző értékeinek hatása is a túlélési függvényre. Az egyes magyarázó változók vizsgálatával komplexebb képet alkothatunk arról, hogy mi befolyásolja az ügyfelek elpártolását, így az ügyfélkör megtartását célzó kampányokat hatékonyabban lehet végrehajtani.
Vidd magaddal
A blogposztunkban bemutatott kódokat és ábrákat elérhetővé tettük egy jupyter notebookban, amit itt találsz meg. Ha bármi kérdésed felmerül, vagy ötleted van, keress minket bátran!
Referenciák
- Anurag Pandey (2019). Survival Analysis: Intuition & Implementation in Python. Towards Data Science blog.
- CamDavidsonPilon/lifelines: v0.24.16.
- Laura Löschmann, Daria Smorodina. (2020). Deep Learning for Survival Analysis. SEMINAR INFORMATION SYSTEMS (WS19/20).
- Lisa Sullivan. Survival Analysis. Boston University School of Public Health.

 Vissza a blogbejegyzésekhez
Vissza a blogbejegyzésekhez